Lecture 4 足球比赛与商业合作的最佳对策

紧跟上节课的后半节的例子，进一步讲述最佳对策的思考方式。

足球比赛

收益矩阵：

$u_1(L,r) = 4$表示有40%的概率进球。

通过计算没有最佳对策。

还是通过概率进行计算。

为什么守门的时候没有中路不动呢？通过后面的计算就能知道为什么了。

假设守门员守左边的概率为p，那么右边的概率为1-p.

那么射手采取L的策略的期望为9-5p。

M：6

R：4+5P

画出来的预期收益的曲线如下：

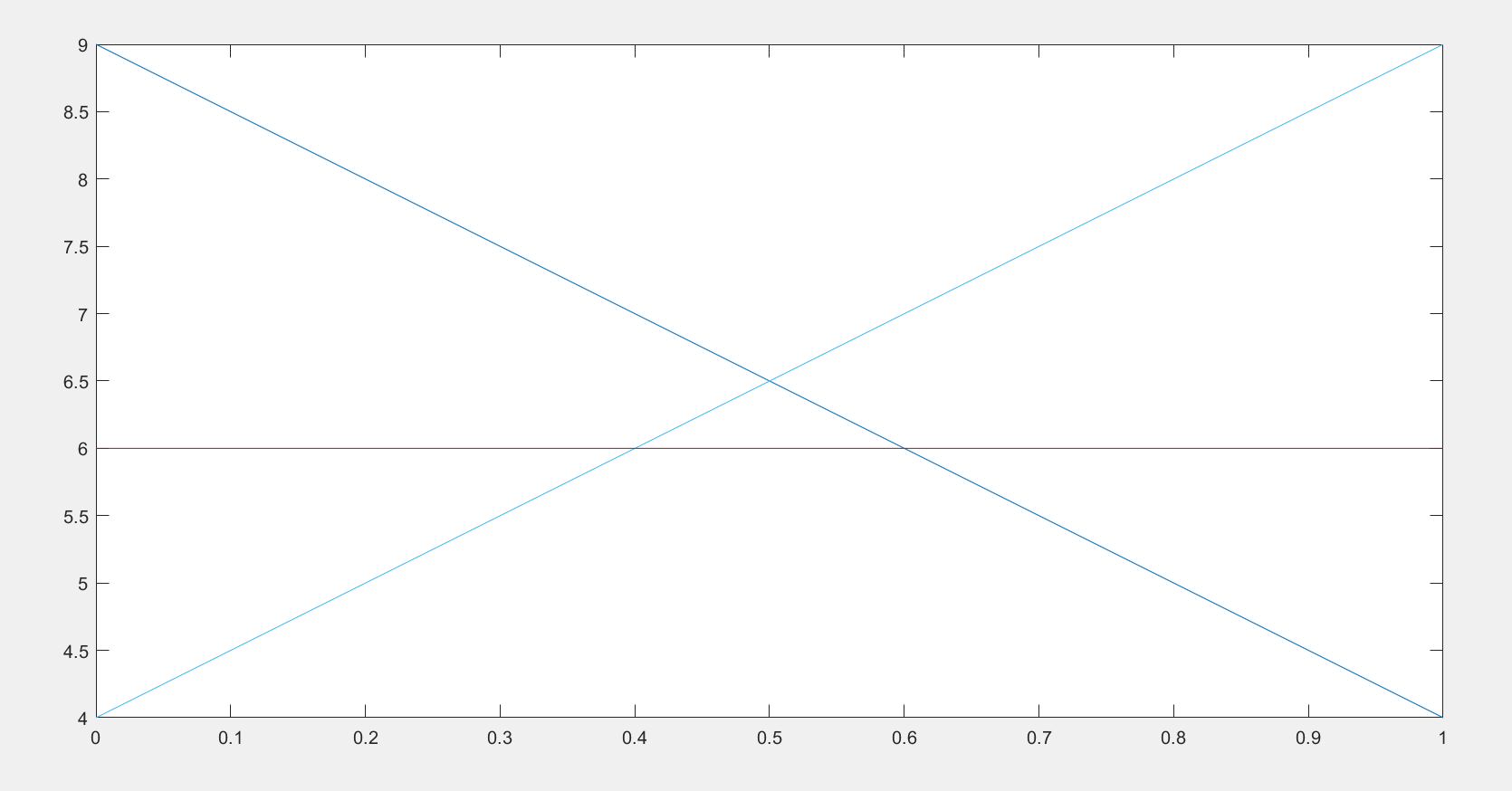
可以发现，如果射中间，那么收益始终是比其他的两种选择收益低的。因此射门员不会选择射中间的门。

千万不要选择在所有情况下都没有最佳对策的决策，像这个例子中，射中间就不能选择。

合伙人博弈

• 两个合伙人每人分享50%的总收益
• 每一个合伙人可以选择投入的精力为$s_i$，并且在[0, 4]这个区间。
• 总收益为$4*(s_1+s_2+b*s_1*s_2)$, $b$在[0, 1/4]之间

$u_1(s_1, s_2) = \frac{1}{2}(4*(s_1+s_2+b*s_1*s_2))-s_1^2$

最后一项是他的付出，至于为什么最后一项是平方，应该就是问题的设计。

同理也能计算$u_2(s_1, s_2)$

为了求上面式子的极值，我们对式子进行求导：

$max_{s_1} 2(s_1+s_2+b*s_1*s_2)-s_1^2$ 进行求导为0： $2*(1+b*s_2)-2*s_1 = 0\\ s_1 = 1+b*s_2$

令b = 1/4, 我们将收益的图画出来：

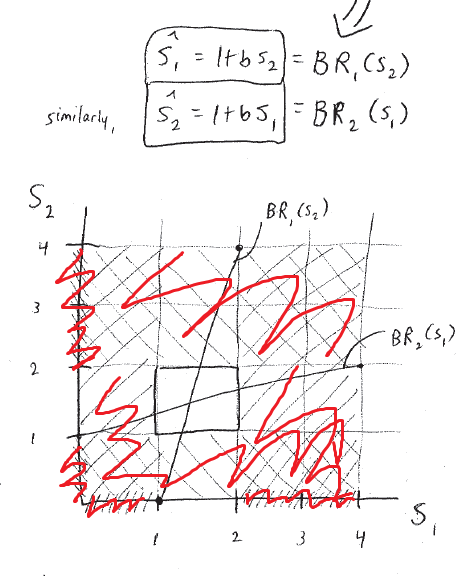
首先当$s_2 = 0$时，$s_1$不会小于1，因为小于1会减少自己的收益，同理，当$s_2 = 4$时，$s_1$也不会大于2。因为此刻努力增加是不会增加自己的收益的。

因此每一个选择的区间都在[1, 2]之间，只剩下一个小的方块。

将图中的那个小方块单独拿出来，接着画出收益曲线：

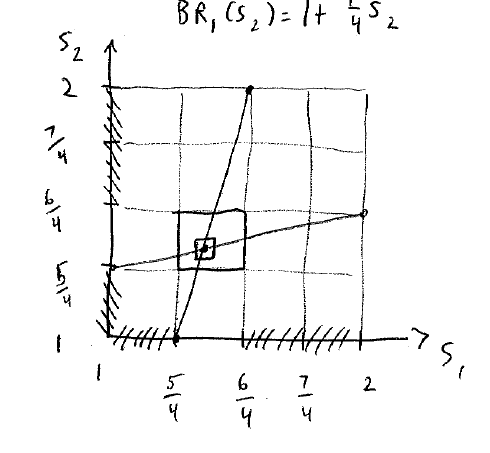
发现我们依旧能够删去一些区间。

最终我们能够通过递归的删除，得到最终的最有对策，就是图中的交点。

最终最优解就是$s_1^* = s_2^* = \frac{1}{1-b}$

这样的组合往往收益是非常低的。

因为在边际成本中，我仅能够获得一半的回报。在经济学中称之为externality。

我们这个时候可以看到b表示的是人之间的协同程度。

如果减小b，根据上面求出的最优解，那么直线的交点就会减小。

这个例子就是传说中的纳什均衡。

结论：The players are playing a best response to each other.